Arbre et arbre inverse

Les images et vidéos stéréoscopiques croisées de ce site permettent la vision en relief, et demandent seulement un léger entraînement de la part de l'observateur. L'oeil gauche doit regarder la figure droite et l'oeil droit doit regarder la figure gauche. Pour cela, on peut fermer d'abord son oeil gauche puis placer sa main droite à quelques centimètres de son oeil droit de façon à lui cacher la figure droite. De même, on ferme l'oeil droit et on place la main gauche à quelques centimètres de son oeil gauche de façon à lui cacher la figure gauche. Les deux yeux étant ouverts, chacun d'eux ne voit qu'une figure. On louche quelque part dans l'intervalle entre les deux mains pour faire superposer les deux figures en une figure unique. Avec un peu d'entraînement, le cerveau finit au bout de quelques secondes à une minute par accommoder la vision sur une figure nette en relief.

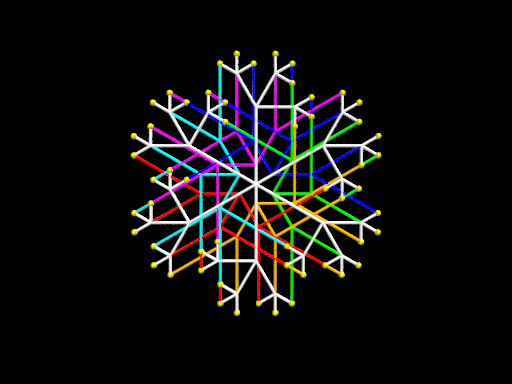
Les dessins illustrent le théorème dit Inverse Tree Theorem¹.

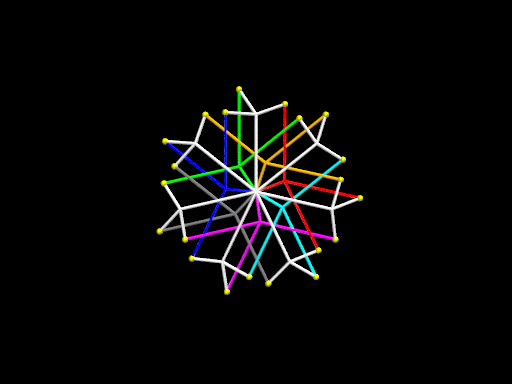
Détaillons le premier dessin. On y voit en blanc un arbre ternaire dont six branches sont issues du centre, chaque branche se divisant en trois sous-branches et celles-ci se divisant encore en trois. On arrête à ce niveau les itérations pour des raisons de lisibilité mais on aurait pu continuer. La longueur d’une sous-branche par rapport à la longueur de la branche dont elle est issue est dans un rapport r inférieur à 1, constant à chaque subdivision. Les trois angles des sous-branches par rapport à la direction de la branche sont également les mêmes à chaque subdivision (ici -30°, 30°, 90°). Ces angles différent entre eux de 60° ou 120°, et ces dernières valeurs engendrent un groupe G de six éléments modulo 360°, à savoir les six multiples de 60°. L’ordre de ce groupe, égal à six, est la raison pour laquelle l’arbre blanc possède six branches au départ. Les feuilles finales de l’arbre blanc sont représentées par des petites boules.
Cet arbre est associé à un arbre dit inverse, construit de la façon suivante. Ses six branches initiales (de six couleurs différentes) sont choisies de telles façon qu’elles aient même longueur et même orientation que les sous-branches finales de l’arbre initial. Lors d’une subdivision, les sous-branches de l’arbre inverse ont une longueur multipliée par 1/r par rapport à la longueur de la branche qu’elles suivent, et les trois angles que forment ces sous-branches par rapport à la direction de la branche sont les opposés des angles de l’arbre blanc.
Le Inverse Tree Theorem énonce alors que, si G est un groupe fini, les deux arbres ainsi construits ont exactement les mêmes feuilles.

Pour mieux distinguer les deux arbres, nous les faisons sortir du plan en éloignant l’une de l’autre les racines des arbres. Nous pouvons alors avoir une vision en trois dimensions de la situation, et observer les deux arbres alternativement en faisant pivoter la figure.

Ci-dessous, on donne d’autres exemples d’arbre binaires ou ternaires, avec 3, 4, 5, 6, 7, ou 8 branches initiales, et une récursivité entre 1 et 3 niveaux, suivis d’une animation de la vue stéréoscopique en 3D donnée plus haut.

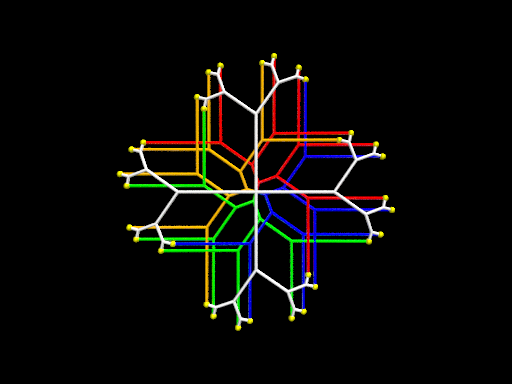
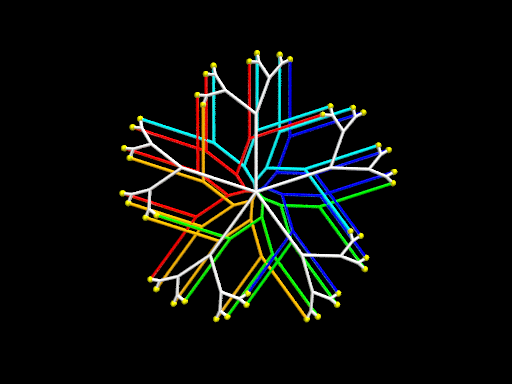
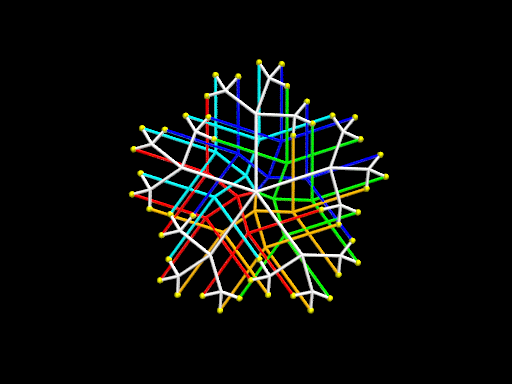
Pour plus de détails, voir : Vince Matsko, Nick Mendler, Symmetric Binary Trees with Branching Ratios Larger than 1, Bridges 2017 Conference Proceedings, ou bien, par les mêmes auteurs, Inverse Tree Theorem, XXVIII:4, Math Horizons (avril 2021), 14-15. ↩︎

Pour accéder à d'autres images stéréoscopiques, cliquer sur l'une des images mignatures ci-dessous. Si vous appréciez ces images et leur animation, vous pouvez une photo de votre ville.