Graphe de Cayley du groupe dicyclique Dic6
Les images et vidéos stéréoscopiques croisées de ce site permettent la vision en relief, et demandent seulement un léger entraînement de la part de l'observateur. L'oeil gauche doit regarder la figure droite et l'oeil droit doit regarder la figure gauche. Pour cela, on peut fermer d'abord son oeil gauche puis placer sa main droite à quelques centimètres de son oeil droit de façon à lui cacher la figure droite. De même, on ferme l'oeil droit et on place la main gauche à quelques centimètres de son oeil gauche de façon à lui cacher la figure gauche. Les deux yeux étant ouverts, chacun d'eux ne voit qu'une figure. On louche quelque part dans l'intervalle entre les deux mains pour faire superposer les deux figures en une figure unique. Avec un peu d'entraînement, le cerveau finit au bout de quelques secondes à une minute par accommoder la vision sur une figure nette en relief.
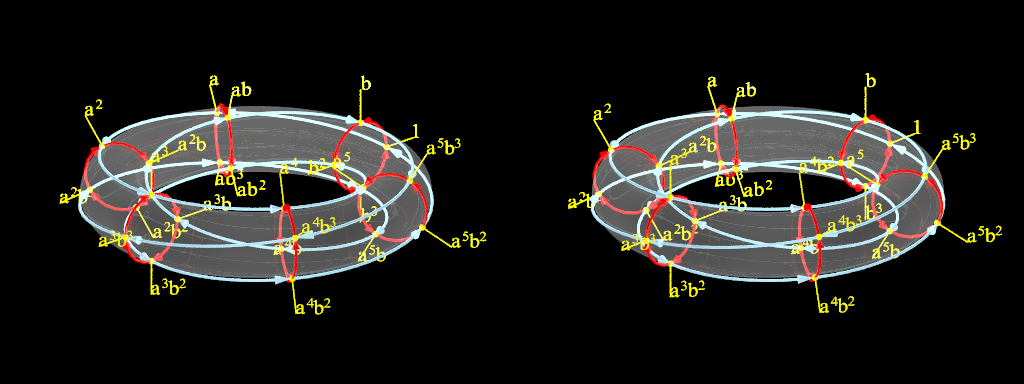
On présente ici le graphe de Cayley du groupe dicyclique Dic6. Ce groupe multiplicatif est engendré par deux éléments a et b vérifiant les règles de calcul suivantes : a6 = b2, b4 = 1, ba = a-1b. Ces règles permettent de représenter les 24 éléments de Dic6 sous la forme akbl, avec k variant de 0 à 5 et l de 0 à 3. On peut considérer par exemple que a est le quaternion cos(iπ/6) + isin(iπ/6), et b le quaternion j.
Dans la figure précédente ou l’animation suivante, chaque sommet jaune du graphe correspond à un élément du groupe. Le graphe de Cayley est construit de la façon suivante. Si on passe d’un élément à un autre par une multiplication à droite par a, on dessine une arête fléchée bleue claire. Si c’est en multipliant à droite par b, on dessine une arête fléchée rouge. Le graphe obtenu comporte 24 rectangles curvilignes et 6 cercles qui peuvent s’inclure dans un tore. Chaque sommet est commun à quatre rectangles et un cercle.
Il est rare qu’un graphe de Cayley puisse être représenté dans le plan ou dans l’espace. Un cas d’impossibilité d’une telle présentation est donnée par le groupe symétrique S4, lui aussi d’ordre 24, et engendré par les transpositions (1 2), (1 3) et (1 4).
Pour accéder à d'autres images stéréoscopiques, cliquer sur l'une des images mignatures ci-dessous. Si vous appréciez ces images et leur animation, vous pouvez une photo de votre ville.