Graphe de Cayley de S4 (IV)
Les images et vidéos stéréoscopiques croisées de ce site permettent la vision en relief, et demandent seulement un léger entraînement de la part de l'observateur. L'oeil gauche doit regarder la figure droite et l'oeil droit doit regarder la figure gauche. Pour cela, on peut fermer d'abord son oeil gauche puis placer sa main droite à quelques centimètres de son oeil droit de façon à lui cacher la figure droite. De même, on ferme l'oeil droit et on place la main gauche à quelques centimètres de son oeil gauche de façon à lui cacher la figure gauche. Les deux yeux étant ouverts, chacun d'eux ne voit qu'une figure. On louche quelque part dans l'intervalle entre les deux mains pour faire superposer les deux figures en une figure unique. Avec un peu d'entraînement, le cerveau finit au bout de quelques secondes à une minute par accommoder la vision sur une figure nette en relief.
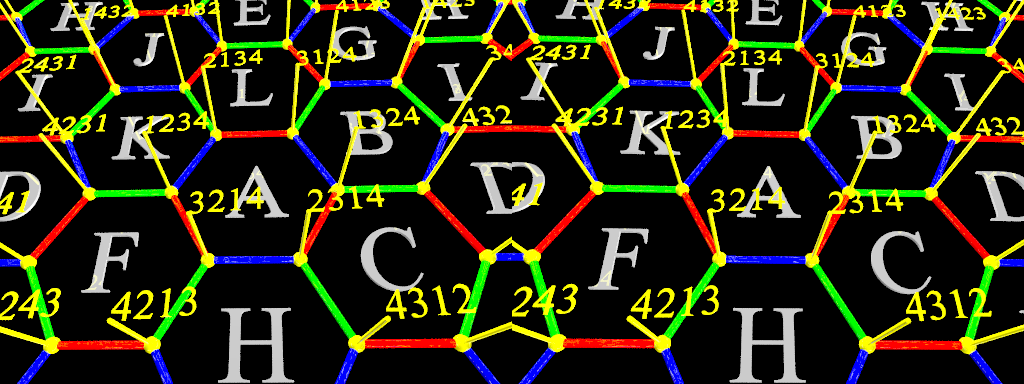
On présente ici le graphe de Cayley du groupe symétrique S4 (groupe des permutations de quatre objets), relativement au système générateur constitué des transpositions (1 2), (1 3) et (1 4).
Dans la figure précédente ou l’animation suivante, chaque sommet jaune du graphe correspond à une des permutations des quatre objets auxquels on a attribué un numéro de 1 à 4. Si on passe d’une permutation à une autre en permutant les numéros de rang 1 et 2, on dessine une arête bleue. Si c’est en permutant les numéros de rang 1 et 3, on dessine une arête rouge. Et si c’est en permutant les numéros de rang 1 et 4, on dessine une arête verte. On obtient alors un graphe constitué de 12 hexagones réguliers, désignés par les lettres de A à L. Chaque sommet est commun à trois hexagones et chaque arête est commune à deux hexagones. Il est nécessaire pour cela que les 12 hexagones soient disposés dans un espace topologique particulier qui se recolle bord à bord. Dans l’animation, on parcourt cet espace par un long travelling qui survole les 12 hexagones les uns après les autres. Le fait qu’on puisse passer d’un sommet quelconque à un autre par une suite d’arêtes est une preuve qu’on peut ranger quatre objets quelconques dans n’importe quel ordre en utilisant plusieurs fois de suite les permutations des objets de rang 1 et 2, ou de rang 1 et 3, ou de rang 1 et 4. C’est une preuve que le groupe symétrique S4 est engendré par les permutations (1 2), (1 3) et (1 4).
On trouvera d’autres graphes de Cayley de S4 (plus simples à comprendre) en consultant les pages Graphe de Cayley de S4 (I), Graphe de Cayley de S4 (II) ou Graphe de Cayley de S4 (III).
Pour accéder à d'autres images stéréoscopiques, cliquer sur l'une des images mignatures ci-dessous. Si vous appréciez ces images et leur animation, vous pouvez une photo de votre ville.