Graphe de Cayley du produit semi-direct Z/3Z ⋊ Z/8Z
Les images et vidéos stéréoscopiques croisées de ce site permettent la vision en relief, et demandent seulement un léger entraînement de la part de l'observateur. L'oeil gauche doit regarder la figure droite et l'oeil droit doit regarder la figure gauche. Pour cela, on peut fermer d'abord son oeil gauche puis placer sa main droite à quelques centimètres de son oeil droit de façon à lui cacher la figure droite. De même, on ferme l'oeil droit et on place la main gauche à quelques centimètres de son oeil gauche de façon à lui cacher la figure gauche. Les deux yeux étant ouverts, chacun d'eux ne voit qu'une figure. On louche quelque part dans l'intervalle entre les deux mains pour faire superposer les deux figures en une figure unique. Avec un peu d'entraînement, le cerveau finit au bout de quelques secondes à une minute par accommoder la vision sur une figure nette en relief.
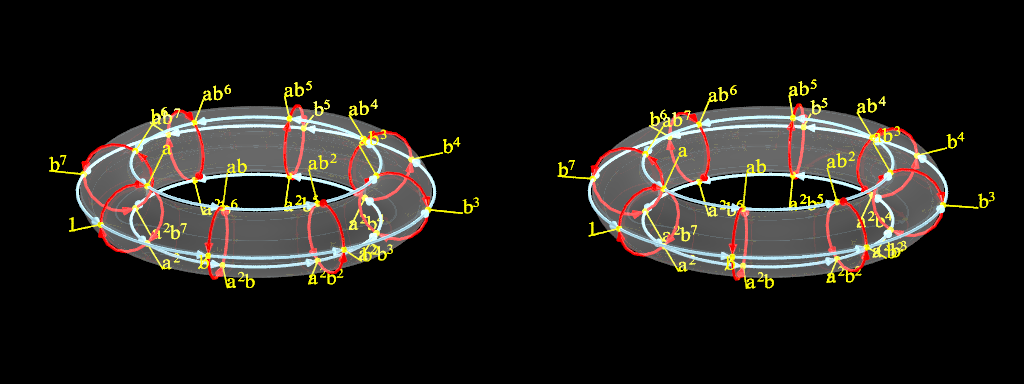
On présente ici le graphe de Cayley du produit semi-direct du groupe cyclique Z/3Z d’ordre 3 par le groupe cyclique Z/8Z d’ordre 8, noté Z/3Z ⋊ Z/8Z. Si on note multiplicativement les lois des deux groupes cycliques, le premier est engendré par un élément a vérifiant a3 = 1, et le second par un élément b tel que b8 = 1. Le produit semi-direct entre Z/3Z et Z/8Z se traduit par la règle supplémentaire ba = a-1b (pour un simple produit direct, on aurait pris Z/3Z commutant avec Z/8Z, soit ba = ab). Ces règles permettent de représenter les 24 éléments de Z/3Z ⋊ Z/8Z sous la forme akbl, avec k variant de 0 à 2 et l de 0 à 7.
Dans la figure précédente ou l’animation suivante, chaque sommet jaune du graphe correspond à un élément du groupe. Le graphe de Cayley est construit de la façon suivante. Si on passe d’un élément à un autre par une multiplication à droite par a, on dessine une arête fléchée rouge. Si c’est en multipliant à droite par b, on dessine une arête fléchée bleue claire. On notera l’alternance des orientations des cercles rouges quand la puissance de b augmente. Le graphe est inclus dans un tore.
Un autre exemple de produit semi-direct d’ordre 24 est donné par Z/3Z ⋊ D4, où D4 est un groupe diédral. On pourrait par ailleurs penser à des variantes de Z/3Z ⋊ Z/8Z, basées sur le même type de définition, mais ce n’est pas si immédiat. Z/4Z ⋊ Z/6Z, par exemple, est en fait isomorphe au produit, direct cette fois, de Z/3Z par D4.
Pour accéder à d'autres images stéréoscopiques, cliquer sur l'une des images mignatures ci-dessous. Si vous appréciez ces images et leur animation, vous pouvez une photo de votre ville.