Conique (I)

Les images et vidéos stéréoscopiques croisées de ce site permettent la vision en relief, et demandent seulement un léger entraînement de la part de l'observateur. L'oeil gauche doit regarder la figure droite et l'oeil droit doit regarder la figure gauche. Pour cela, on peut fermer d'abord son oeil gauche puis placer sa main droite à quelques centimètres de son oeil droit de façon à lui cacher la figure droite. De même, on ferme l'oeil droit et on place la main gauche à quelques centimètres de son oeil gauche de façon à lui cacher la figure gauche. Les deux yeux étant ouverts, chacun d'eux ne voit qu'une figure. On louche quelque part dans l'intervalle entre les deux mains pour faire superposer les deux figures en une figure unique. Avec un peu d'entraînement, le cerveau finit au bout de quelques secondes à une minute par accommoder la vision sur une figure nette en relief.

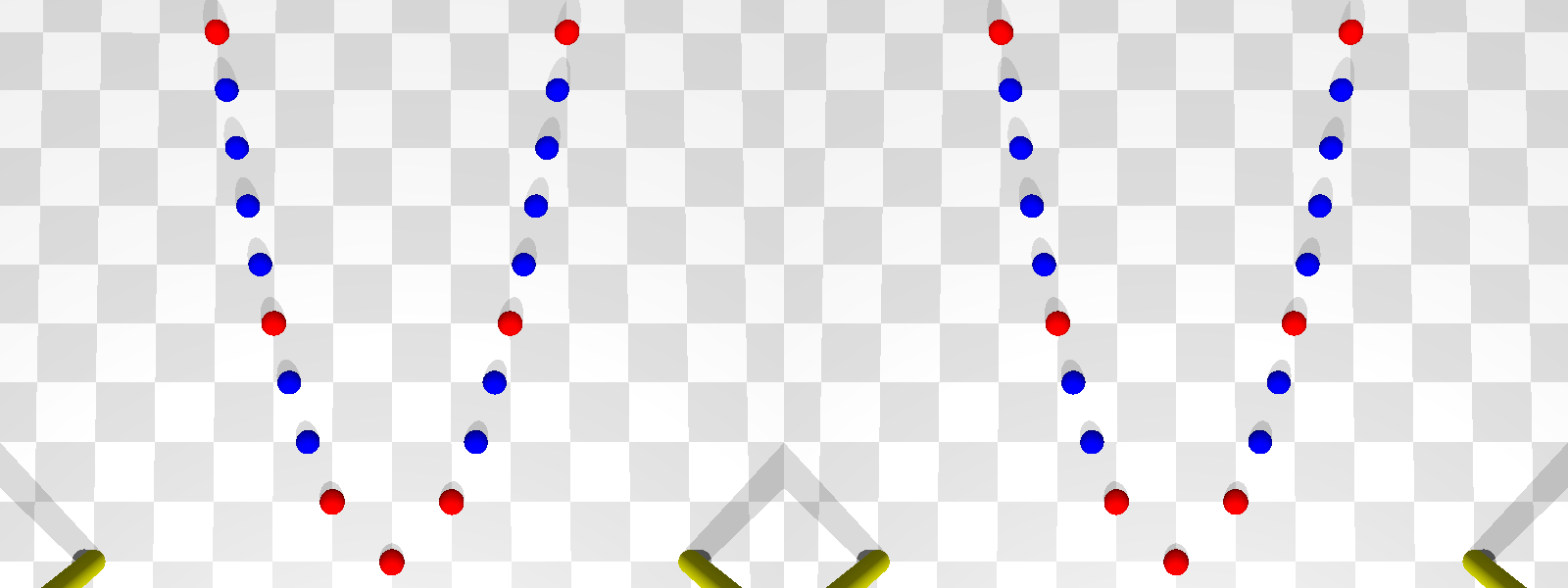
Les points bleus de la première figure ci-dessus semblent alignés sur une ellipse. Pourtant ils le sont selon une parabole, comme le montre la deuxième figure. L'ellipse apparente est une parabole, disposée sur un plan horizontal, mais vue en perspective. On pourra constater que les points rouges sont aux coordonnées (n, n²) avec n entier. Les points bleus sont aux coordonnées (x, x²) avec x non entier, mais x² entier. Les bâtons jaunes sont disposés aux sommets de carrés successifs de côtés 10. Mais si une parabole peut être vue sous forme d'ellipse, y a-t-il un point de vue où on la voit sous forme d'hyperbole ? La réponse est positive. Ainsi, en géométrie projective, il n'y a qu'un seul type de conique et non trois.

Pour accéder à d'autres images stéréoscopiques, cliquer sur l'une des images mignatures ci-dessous. Si vous appréciez ces images et leur animation, vous pouvez une photo de votre ville.