Cube et son dual
Les images et vidéos stéréoscopiques croisées de ce site permettent la vision en relief, et demandent seulement un léger entraînement de la part de l'observateur. L'oeil gauche doit regarder la figure droite et l'oeil droit doit regarder la figure gauche. Pour cela, on peut fermer d'abord son oeil gauche puis placer sa main droite à quelques centimètres de son oeil droit de façon à lui cacher la figure droite. De même, on ferme l'oeil droit et on place la main gauche à quelques centimètres de son oeil gauche de façon à lui cacher la figure gauche. Les deux yeux étant ouverts, chacun d'eux ne voit qu'une figure. On louche quelque part dans l'intervalle entre les deux mains pour faire superposer les deux figures en une figure unique. Avec un peu d'entraînement, le cerveau finit au bout de quelques secondes à une minute par accommoder la vision sur une figure nette en relief.
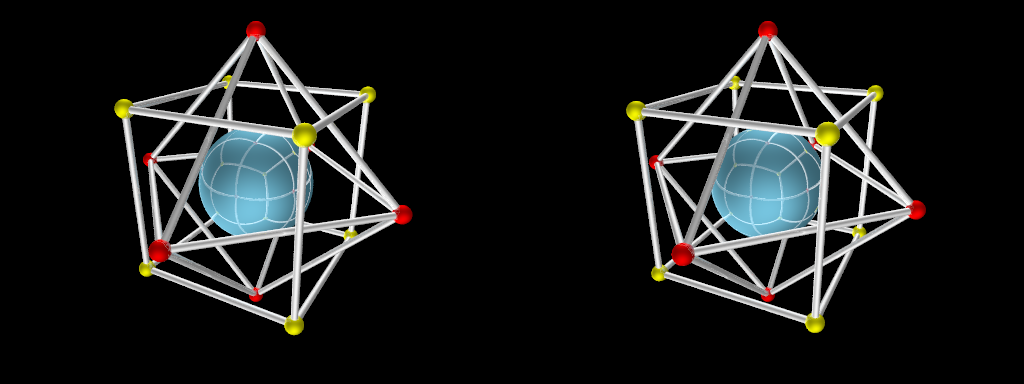
Etant donné un polyèdre, le dual de celui-ci est un autre polyèdre obtenu en échangeant les mots :
“face” et “sommet”
“arête appartenant à une face” en “arête possédant un sommet”
“sommet appartenant à une face” en “face possédant un sommet”
“arête commune à deux faces” en “arête reliant deux sommets”
“sommet appartenant à une arête” en “face possédant une arête”
Ainsi, le cube est un polyèdre constitué de 6 faces, 12 arêtes, 8 sommets. Chaque face possède 4 arêtes. Chaque sommet appartient à 3 arêtes et à 3 faces.
Le dual du cube est constitué de 6 sommets, 12 arêtes, 8 faces. Chaque sommet appartient à 4 arêtes. Chaque face possède 3 arêtes et 3 sommets. Le polyèdre dual ainsi décrit est l’octaèdre.
Le dual de l’octaèdre redonne le cube. Ci-dessus, on a représenté l’octaèdre et le cube, chaque sommet de l’un correspondant à une face de l’autre. La sphère centrale est purement décorative. Ci-dessous, l’animation tente de visualiser le passage d’un polyèdre à son dual en transformant les faces en sommets.
D’autres exemples de polyèdres duaux sont donnés par la géode et la géode duale, par le dodécaèdre et l’icosaèdre, ou par le tétraèdre qui est son propre dual.
Pour accéder à d'autres images stéréoscopiques, cliquer sur l'une des images mignatures ci-dessous. Si vous appréciez ces images et leur animation, vous pouvez une photo de votre ville.