Duplication du cube
Les images et vidéos stéréoscopiques croisées de ce site permettent la vision en relief, et demandent seulement un léger entraînement de la part de l'observateur. L'oeil gauche doit regarder la figure droite et l'oeil droit doit regarder la figure gauche. Pour cela, on peut fermer d'abord son oeil gauche puis placer sa main droite à quelques centimètres de son oeil droit de façon à lui cacher la figure droite. De même, on ferme l'oeil droit et on place la main gauche à quelques centimètres de son oeil gauche de façon à lui cacher la figure gauche. Les deux yeux étant ouverts, chacun d'eux ne voit qu'une figure. On louche quelque part dans l'intervalle entre les deux mains pour faire superposer les deux figures en une figure unique. Avec un peu d'entraînement, le cerveau finit au bout de quelques secondes à une minute par accommoder la vision sur une figure nette en relief.
Theon de Smyrne, dans son Exposition des connaissances mathématiques pour la lecture de Platon, rapporte que, selon Eratosthène, « les Déliens, ayant interrogé l’oracle sur les moyens de se délivrer de la peste, le dieu leur ordonna de construire un autel double de celui qui existait déjà. Ce problème jeta les architectes dans un étrange embarras. Ils se demandaient comment faire un solide double d’un autre. Ils interrogèrent Platon sur la difficulté. Celui-ci leur répondit que le dieu avait ainsi rendu l’oracle, non qu’il eût besoin d’un autel double, mais pour reprocher aux Grecs de négliger l’étude des mathématiques et de faire peu de cas de la géométrie ».
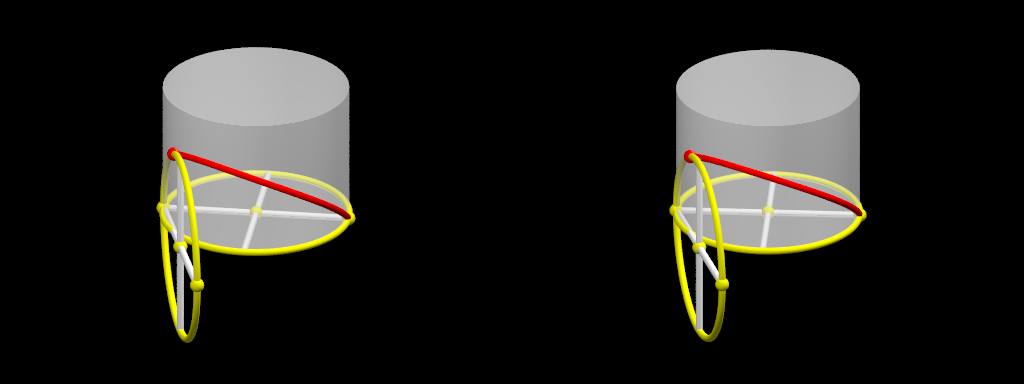
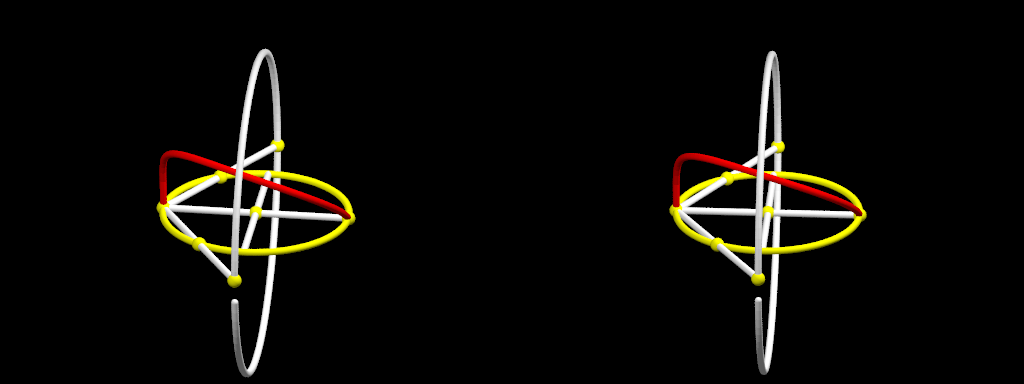
Double est à prendre ici au sens du volume. À supposer que l’autel initial soit un cube, on obtient le problème antique de la duplication du cube : étant donné un segment de longueur 1, construire un segment de longueur la racine cubique de 2. Les tentatives d’une telle construction à la règle et au compas restèrent vaines pendant 2000 ans, jusqu’à ce que l’impossibilité d’une telle construction soit prouvée au XIXème siècle. Cependant, des constructions utilisant d’autres outils ont été proposées dès l’Antiquité. En particulier, Archytas de Tarente utilisa, dans l’espace de dimension 3, l’intersection d’un cylindre, d’un tore et d’un cône pour obtenir un point permettant d’obtenir la construction cherchée.
Les deux images précédentes sont des étapes de cette construction, décrite par l’animation ci-dessous. Le tore n’est pas représenté, mais seulement illustré par la rotation du cercle vertical qui l’engendre. Au cours de cette rotation, l’intersection du cercle et du cylindre engendre une courbe (rouge dans l’animation), dite courbe d’Archytas, intersection du cylindre et du tore. De même, le cône n’est pas représenté, mais seulement illustré par le mouvement d’une de ses génératrices. Cette génératrice rencontre la courbe d’Archytas en un point, dont la projection dans le plan du cercle de base du cylindre permet de construire le côté désiré. Le lecteur est invité à prouver par le calcul cette conclusion.
Pour accéder à d'autres images stéréoscopiques, cliquer sur l'une des images mignatures ci-dessous. Si vous appréciez ces images et leur animation, vous pouvez une photo de votre ville.