Géométrie projective sur un corps fini

Les images et vidéos stéréoscopiques croisées de ce site permettent la vision en relief, et demandent seulement un léger entraînement de la part de l'observateur. L'oeil gauche doit regarder la figure droite et l'oeil droit doit regarder la figure gauche. Pour cela, on peut fermer d'abord son oeil gauche puis placer sa main droite à quelques centimètres de son oeil droit de façon à lui cacher la figure droite. De même, on ferme l'oeil droit et on place la main gauche à quelques centimètres de son oeil gauche de façon à lui cacher la figure gauche. Les deux yeux étant ouverts, chacun d'eux ne voit qu'une figure. On louche quelque part dans l'intervalle entre les deux mains pour faire superposer les deux figures en une figure unique. Avec un peu d'entraînement, le cerveau finit au bout de quelques secondes à une minute par accommoder la vision sur une figure nette en relief.

Les corps finis sont des ensembles finis munis d’une addition et d’une multiplication. Tout élément non nul y admet un inverse. Le plus simple des corps finis est F₂ = Z/2Z. Il possède seulement deux éléments, notés 0 et 1. La seule règle de calcul inhabituelle intervient dans la somme. On a en effet : 1 + 1 = 0, ou encore 1 = -1. Si on préfère, on peut remplacer 0 par pair et 1 par impair. La somme et le produit sont alors les opérations qui décrivent comment se comporte la parité lorsqu’on ajoute ou qu’on multiplie deux entiers. Ainsi, la règle 1 + 1 = 0 exprime que impair + impair = pair.

On peut appliquer sur ce corps une géométrie comparable à la géométrie usuelle. Il suffit d’y remplacer le corps R des réels par le corps F₂. Par exemple, l’espace affine de dimension 3 sur F₂ comporte huit éléments, qui sont (0,0,0), (0,0,1), (0,1,0), etc. (1,1,1). On peut visualiser ces huit éléments en les disposant aux sommets d’un cube, mais il convient de bien avoir conscience que les seuls éléments de l’espace affine de dimension 3 sur F₂ sont ces huit sommets, et rien d’autre. Une droite reliant deux points n’est rien d’autre que la réunion de ces deux points. Même si on décide de visualiser cette droite dans l’espace usuel R³ en reliant ces deux points par un segment ou une droite de R³ (ou même une courbe passant par ces deux points), ce n’est que par commodité qu’on agit ainsi, aucun élément de ce segment, de cette droite ou de cette courbe n’existe dans F₂³ en dehors des deux points initiaux. Par exemple, les droites {(0,0,0), (0,1,1)} et {(0,1,0), (0,0,1)}, qui sont les deux diagonales d’une face du cube, sont parallèles dans F₂³. En effet, la première droite a pour vecteur directeur (0,1,1) et la deuxième droite a pour vecteur directeur (0,-1,1) qui est bien égal à (0,1,1) puisque -1 = 1 dans F₂.

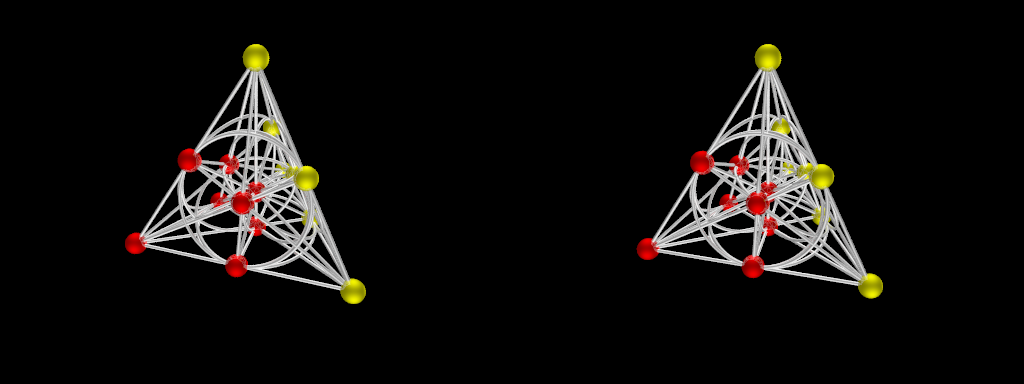
La géométrie projective, quant à elle, est une géométrie dans laquelle on ne fait pas de distinction entre droites sécantes et droites parallèles. Pour obtenir un espace projectif à partir d’un espace affine, on rajoute pour chaque ensemble de droites parallèles un point dit à l’infini qui sera le point commun aux droites initialement parallèles. Dans la figure ci-dessus, les sphères rouges sont les huit points de l’espace affine F₂³. On vérifiera que, dans cet espace, il y a 28 droites, formant sept sous-ensembles de quatre droites parallèles entre elles. Pour obtenir l’espace projectif correspondant, on doit donc rajouter sept points, qui sont les sphères jaunes. On peut constater que quatre côtés parallèles du cube rouge se rencontrent effectivement en un unique point jaune. Pour visualiser les droites de l’espace ainsi obtenu, il a parfois été nécessaire de recourir à des cercles, par exemple pour représenter certaines diagonales d’une face du cube rouge.

Dans l’animation ci-dessous, toutes les sphères sont en jaune car, dans l’espace projectif, tous les points jouent des rôles parfaitement symétriques. On peut donc aussi tracer des droites formés de points à l’infini, le nombre total de droites de l’espace projectif étant alors de 35.

Pour accéder à d'autres images stéréoscopiques, cliquer sur l'une des images mignatures ci-dessous. Si vous appréciez ces images et leur animation, vous pouvez une photo de votre ville.