Hyper-120-Cell
Les images et vidéos stéréoscopiques croisées de ce site permettent la vision en relief, et demandent seulement un léger entraînement de la part de l'observateur. L'oeil gauche doit regarder la figure droite et l'oeil droit doit regarder la figure gauche. Pour cela, on peut fermer d'abord son oeil gauche puis placer sa main droite à quelques centimètres de son oeil droit de façon à lui cacher la figure droite. De même, on ferme l'oeil droit et on place la main gauche à quelques centimètres de son oeil gauche de façon à lui cacher la figure gauche. Les deux yeux étant ouverts, chacun d'eux ne voit qu'une figure. On louche quelque part dans l'intervalle entre les deux mains pour faire superposer les deux figures en une figure unique. Avec un peu d'entraînement, le cerveau finit au bout de quelques secondes à une minute par accommoder la vision sur une figure nette en relief.
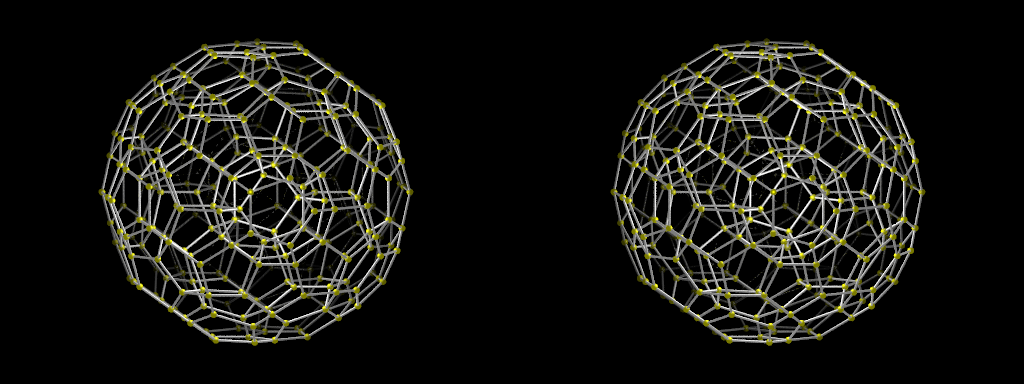
En dimension 3, il existe cinq polyèdres réguliers, connus depuis Platon : le tétraèdre, l’octaèdre, le cube, le dodécaèdre et l’icosaèdre. En dimension 4, on parle de 4-polytopes. Il existe six 4-polytopes convexes réguliers, cinq d’entre eux étant les généralisations directes des cinq polyèdres réguliers, mais il en existe un sixième n’ayant pas d’équivalent en dimension 3. Comment les visualiser ? Puisqu’on peut représenter les polyèdres tridimensionnels en les représentant par un dessin plan, on peut aussi représenter les 4-polytopes par un dessin plan. Il suffit pour cela d’utiliser une projection sur un plan parallèlement à un plan supplémentaire. Mais la vision stéréoscopique permet également de représenter un 4-polytope en le projetant dans un espace de dimension 3 parallèlement à une droite supplémentaire. C’est ce que nous faisons dans l’image stéréoscopique ci-dessus.
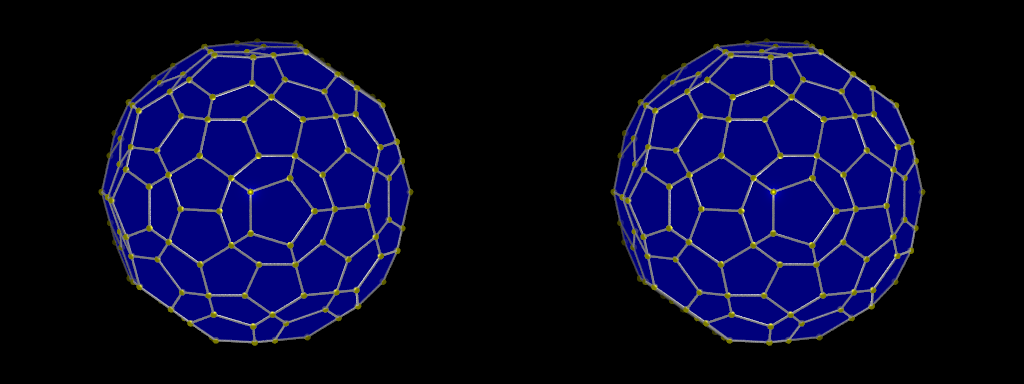
On représente ici le polytope 120-cell (ou hécatonicosachore). Il possède 600 sommets, 1200 arêtes, 720 faces pentagonales et 120 cellules tridimensionnelles en forme de dodécaèdres. Dans la première image ci-dessus, certains sommets restent invisibles car ils sont parfaitement alignés avec d’autres le long de l’axe de vision ou bien ont le même projeté dans l’espace de dimension 3. Dans la seconde figure, on a ajouté les faces ce qui rend la projection de la figure plus visible mais occulte également la majorité du polytope.
Dans un espace de dimension 4, on peut effectuer une rotation simultanément dans deux plans orthogonaux. C’est ce que nous faisons dans l’animation ci-dessous, l’une des vitesses de rotation étant double de l’autre. Le polytope semble se déformer, mais ce n’est qu’une illusion due à la projection que nous en faisons en dimension 3. En réalité, dans l’espace de dimension 4, le polytope reste rigide. Dans l’animation représentant les faces, les projections de certains sommets, avec leurs arêtes, apparaissent ou disparaissent au cours de la rotation car elles sont cachées par les autres faces.
Pour accéder à d'autres images stéréoscopiques, cliquer sur l'une des images mignatures ci-dessous. Si vous appréciez ces images et leur animation, vous pouvez une photo de votre ville.