Courbe de Lebesgue

Les images et vidéos stéréoscopiques croisées de ce site permettent la vision en relief, et demandent seulement un léger entraînement de la part de l'observateur. L'oeil gauche doit regarder la figure droite et l'oeil droit doit regarder la figure gauche. Pour cela, on peut fermer d'abord son oeil gauche puis placer sa main droite à quelques centimètres de son oeil droit de façon à lui cacher la figure droite. De même, on ferme l'oeil droit et on place la main gauche à quelques centimètres de son oeil gauche de façon à lui cacher la figure gauche. Les deux yeux étant ouverts, chacun d'eux ne voit qu'une figure. On louche quelque part dans l'intervalle entre les deux mains pour faire superposer les deux figures en une figure unique. Avec un peu d'entraînement, le cerveau finit au bout de quelques secondes à une minute par accommoder la vision sur une figure nette en relief.

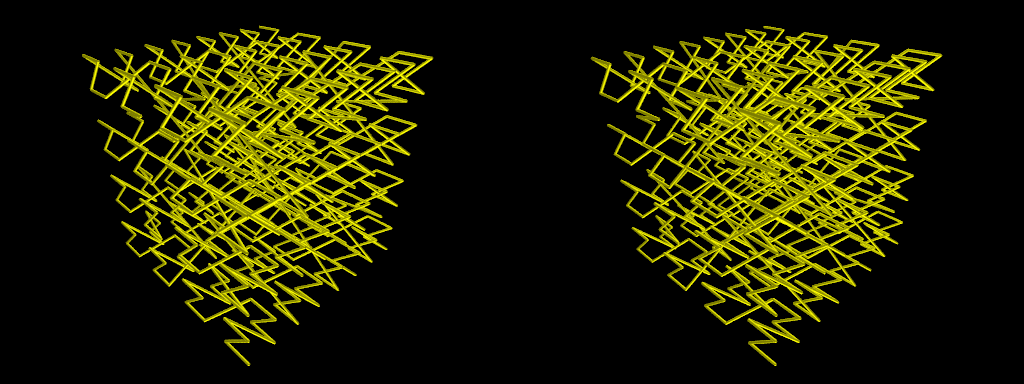
La courbe de Lebesgue est un arc paramétré continu de l’intervalle [0,1] dans le carré [0,1]², ou même dans le cube [0,1]³, comme dans le cas ci-dessus. C’est une courbe dite de remplissage, comme l’est la courbe de Peano, car elle remplit complètement le cube. Elle est construite schématiquement comme suit.

Dans un premier temps, soit u un réel de l’intervalle [0,1], dont le développement binaire est 0.u₁u₂u₃… On lui associe un point de l’espace de dimension 3 dont les coordonnées binaires sont (0.u₁u₄u₇…, 0.u₂u₅u₈…, 0.u₃u₆u₉…). On définit ainsi une application de l’intervalle [0,1] dans le cube [0,1]³. Malheureusement, cette application n’est pas continue. En effet, le réel u = 1/2 a un développement binaire 0.10000000… et aura pour image le point de coordonnées binaires (0.100…, 0, 0), autrement dit le point (1/2, 0, 0). Considérons maintenant la suite de nombres réels légèrement inférieurs à 1/2 et dont le développement binaire est 0.011111… avec un nombre arbitrairement grand de 1. Cette suite tend vers 1/2 quand le nombre de 1 tend vers l’infini, mais son image est constituée des points de coordonnées binaires (0.0111…, 0.111…, 0.111…) qui tend vers (1/2, 1, 1) et non vers (1/2, 0, 0).

Pour rendre l’application continue, on passe par l’intermédiaire de l’ensemble de Cantor, constitué des réels y compris entre 0 et 1 dont le développement en base 3 est constitué uniquement des chiffres 0 et 2. On divise chacun des chiffres ternaires de y par 2 pour obtenir une suite de 0 et de 1, et c’est cette suite qu’on scinde en trois pour obtenir les trois coordonnées binaires d’un point du cube qu’on associera à y. Par exemple, y = 2/3 a pour développement en base 3 la suite 0.2000…. On lui associe la suite des chiffres binaires 0.1000… qu’on scinde en trois, donnant comme point associé à y le point de coordonnées binaires (0.1000…, 0, 0), soit (1/2, 0, 0). Prenons maintenant un nombre de Cantor t strictement inférieur à 1/3 mais arbitrairement proche de 1/3. Son développement ternaire sera par exemple 0.02222… avec un nombre arbitrairement grand de 2. On lui associe la suite des chiffres binaires 0.01111… qui aura pour image le point de coordonnées binaires (0.0111…, 0.111…, 0.111…) qui tend vers (1/2, 1, 1) quand le nombre de chiffres tend vers l’infini. Mais cette fois-ci, (1/2, 0, 0) est l’image de 2/3 et (1/2, 1, 1) est l’image de 1/3. Il est alors loisible de relier continûment les deux points (1/2, 1, 1) et (1/2, 0, 0) par un segment pendant que la valeur du paramètre antécédent d’un point de ce segment varie de 1/3 à 2/3. Ces segments apparaissent dans la figure sous forme de diagonales.

Si les calculs sont menés avec une précision de N chiffres seulement, on obtient une courbe en zig-zag qui parcourt partiellement le cube. C’est le cas de la figure présentée et des animations ci-dessous, le nombre de chiffres utilisés étant de N = 3.

Une variante est donnée par la courbe de Hilbert. Mais contrairement à cette dernière, la fonction paramétrique définissant la courbe de Lebesgue est presque partout dérivable.

Pour accéder à d'autres images stéréoscopiques, cliquer sur l'une des images mignatures ci-dessous. Si vous appréciez ces images et leur animation, vous pouvez une photo de votre ville.