Rotation d'un solide (III)
Les images et vidéos stéréoscopiques croisées de ce site permettent la vision en relief, et demandent seulement un léger entraînement de la part de l'observateur. L'oeil gauche doit regarder la figure droite et l'oeil droit doit regarder la figure gauche. Pour cela, on peut fermer d'abord son oeil gauche puis placer sa main droite à quelques centimètres de son oeil droit de façon à lui cacher la figure droite. De même, on ferme l'oeil droit et on place la main gauche à quelques centimètres de son oeil gauche de façon à lui cacher la figure gauche. Les deux yeux étant ouverts, chacun d'eux ne voit qu'une figure. On louche quelque part dans l'intervalle entre les deux mains pour faire superposer les deux figures en une figure unique. Avec un peu d'entraînement, le cerveau finit au bout de quelques secondes à une minute par accommoder la vision sur une figure nette en relief.
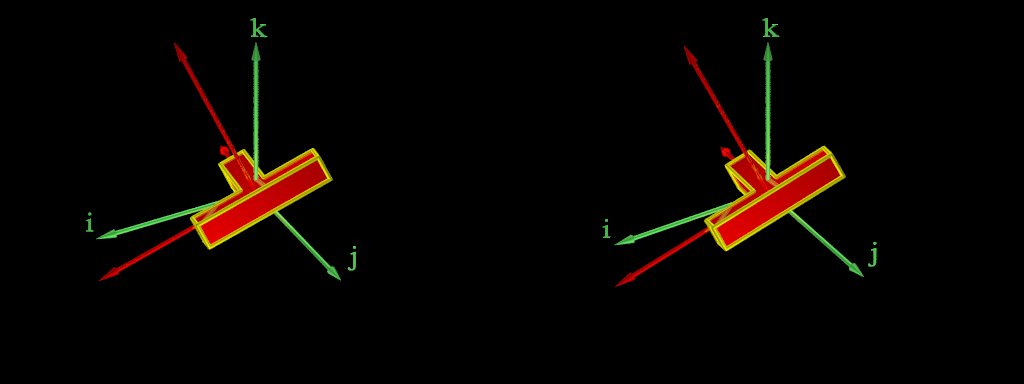

On considère un solide en rotation dans un référentiel (qu’on appellera référentiel initial) dont les axes restent parallèles à un référentiel galiléen, le moment au centre d’inertie des forces qui s’appliquent sur lui étant supposé nul. On sait que, dans ce cas, le moment cinétique est constant. On le supposera colinéaire à l’axe vertical de l’image ci-dessus. La résolution des équations du mouvement augmente en complexité selon que les moments principaux d’inertie sont tous égaux, ou que deux d’entre eux sont égaux, ou qu’ils sont tous les trois distincts.
Le cas le plus difficile est celui où les trois moments principaux d’inertie sont différents. C’est le cas d’un objet quelconque, sans symétrie particulière, mais aussi le cas de l’objet en forme de T représenté ci-dessus. Si le moment cinétique n’est pas aligné avec un axe principal d’inertie, le vecteur de rotation instantanée ne lui est pas colinéaire et il varie avec le temps. La résolution exacte du mouvement nécessite l’utilisation des fonctions elliptiques de Jacobi. Le solide est animé d’un mouvement de nutation, de précession et de rotation propre. On montre que la nutation et la rotation propre sont des fonctions périodiques du temps, de même période. Au cours de cette période, la précession a tourné d’un certain angle et le mouvement se répète relativement à cet angle, mais il n’y a pas de raison que cet angle soit commensurable à un tour complet, de sorte que le mouvement dans le référentiel initial n’est pas en général périodique. Dans la première animation, les valeurs des moments d’inertie ont été choisies pour qu’il le soit.
Enfin, il existe dans le référentiel initial un plan fixe sur lequel l’ellipsoïde d’inertie roule et pivote sans glisser. Le point de contact (par lequel passe le vecteur de rotation instantanée) décrit une courbe (blanche dans l’animation ci-dessous) dans le plan fixe appelée herpolhodie, et une courbe (bleue dans l’animation ci-dessous) dans l’ellipsoïde d’inertie appelée polhodie. La polhodie roule sans glisser sur l’herpolhodie.
Dans la deuxième animation, la vitesse de rotation a été ralentie par rapport à la première animation pour la rendre plus visible.
Pour les deux autres cas, voir les pages Rotation d’un solide (I) et Rotation d’un solide (II).
Pour accéder à d'autres images stéréoscopiques, cliquer sur l'une des images mignatures ci-dessous. Si vous appréciez ces images et leur animation, vous pouvez une photo de votre ville.