Tours de Stockmeyer
Les images et vidéos stéréoscopiques croisées de ce site permettent la vision en relief, et demandent seulement un léger entraînement de la part de l'observateur. L'oeil gauche doit regarder la figure droite et l'oeil droit doit regarder la figure gauche. Pour cela, on peut fermer d'abord son oeil gauche puis placer sa main droite à quelques centimètres de son oeil droit de façon à lui cacher la figure droite. De même, on ferme l'oeil droit et on place la main gauche à quelques centimètres de son oeil gauche de façon à lui cacher la figure gauche. Les deux yeux étant ouverts, chacun d'eux ne voit qu'une figure. On louche quelque part dans l'intervalle entre les deux mains pour faire superposer les deux figures en une figure unique. Avec un peu d'entraînement, le cerveau finit au bout de quelques secondes à une minute par accommoder la vision sur une figure nette en relief.
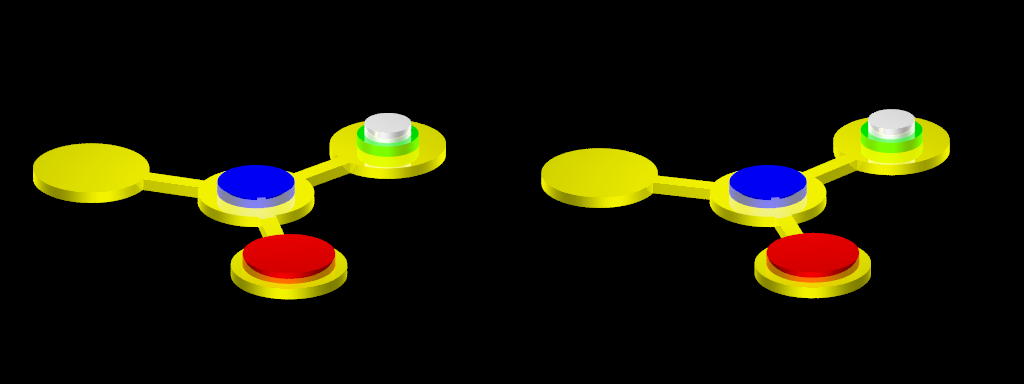
Les tours de Stockmeyer sont une variante des tours de Hanoï. Il s’agit de déplacer une pile de disques, d’une position à une autre, un par un, un disque ne pouvant être placé sur un disque plus petit. Mais dans la version de Stockmeyer, les seuls déplacements autorisés sont ceux d’une position latérale à la position centrale, ou de la position centrale à une position latérale. Ci-dessus, on représente une situation en cours de jeu avec quatre disques, et ci-dessous, une animation présentant une solution complète en 20 déplacements.
Combien y a-t-il de mouvements en fonction du nombre n de disques ? Paul Stockmeyer prouva en 1994 qu’une solution existait avec un nombre de mouvements calculé comme suit : prendre les n premiers entiers (1 compris) dont les facteurs premiers sont 2 ou 3, en faire la somme, puis prendre le double du résultat. Ainsi, pour n = 4, les entiers en question sont 1, 2, 3, 4 de somme 10 et dont le double est 20. Il y a donc une solution en 20 mouvements. En 2017, Thierry Bousch prouva que ce nombre correspondait aux solutions optimales. Saurez-vous trouver les 66 = 2×(1+2+3+4+6+8+9) mouvements nécessaires et suffisants pour déplacer une pile de 7 disques ?
Pour accéder à d'autres images stéréoscopiques, cliquer sur l'une des images mignatures ci-dessous. Si vous appréciez ces images et leur animation, vous pouvez une photo de votre ville.